Análisis de circuito
Entradas populares
martes, 19 de febrero de 2013
lunes, 18 de febrero de 2013
EJERCICIOS CON FORMULAS :
La única tensión desconocida en este circuito es V1. Hay tres conexiones en este nodo y por esta razón, 3 corrientes a considerar. Ahora se analiza todas las corrientes que pasan por el nodo, así:

Con ley de corrientes de Kirchhoff (LCK), tenemos:

Se resuelve con respecto a V1:

Finalmente, la tensión desconocida se resuelve sustituyendo valores numéricos para cada variable. Después de haber obtenido estas ecuaciones y conocer cada tensión, es fácil calcular cualquier corriente desconocida.
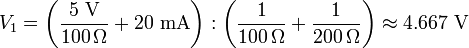
martes, 22 de enero de 2013
PROCEDIMIENTO :
- Localice los segmentos de cable conectados al circuito.
- Seleccione un nodo de referencia (polo a tierra). Se puede elegir cualquier nodo ya que esto no afecta para nada los cálculos; pero elegir el nodo con más conexiones podría simplificar el análisis.
- Identifique los nodos que están conectados a fuentes de voltaje que tengan una terminal en el nodo de referencia. En estos nodos la fuente define la tensión del nodo. Si la fuente es independiente, la tensión del nodo es conocida.
- Asigne una variable para los nodos que tengan tensiones desconocidas. Si la tensión del nodo ya se conoce, no es necesario asignarle una variable.
- Para cada uno de los nodos, se plantean las ecuaciones de acuerdo con las Leyes de Kirchhoff. .
- Si hay fuentes de tensión entre dos tensiones desconocidas, una esos dos nodos como un supernodo , haciendo el sumatorio de todas las corrientes que entran y salen en ese supernodo. Las tensiones de los dos nodos simples en el supernodo están relacionadas por la fuente de tensión intercalada.
- Resuelva el sistema de ecuaciones simultáneas para cada tensión desconocida.
lunes, 21 de enero de 2013
ANÁLISIS DE NODOS .
El análisis de nodos es un método para determinar la tensión de uno o varios nodos.
En el análisis de nodos se escribe una ecuación para cada nodo, con condición que la suma de esas corrientes sea igual a cero. Estas corrientes se escriben en términos de las tensiones de cada nodo del circuito.
El análisis de nodos es posible cuando todos los nodos tienen conductancia. Este método produce un sistema de ecuaciones, que puede resolverse a mano si es pequeño, o también puede resolverse rápidamente por ordenador .
En el análisis de nodos se escribe una ecuación para cada nodo, con condición que la suma de esas corrientes sea igual a cero. Estas corrientes se escriben en términos de las tensiones de cada nodo del circuito.
El análisis de nodos es posible cuando todos los nodos tienen conductancia. Este método produce un sistema de ecuaciones, que puede resolverse a mano si es pequeño, o también puede resolverse rápidamente por ordenador .
martes, 8 de enero de 2013
Formulas .
Las fórmulas se clasifican según los tipos de mallas.
MALLAS:

Casos especiales.
SUPERMALLA:

FUENTES DEPENDIENTES:

MALLAS:

Casos especiales.
SUPERMALLA:

FUENTES DEPENDIENTES:

Como realizar las formulas .
Existen dos pasos :
1- Se prefiere asignarle a todas la corrientes de malla el mismo sentido.
2- Se plantea una ecuación que estará en función de la corriente que circula por cada elemento. Se utiliza para obtener las diferentes corrientes de malla.
1- Se prefiere asignarle a todas la corrientes de malla el mismo sentido.
2- Se plantea una ecuación que estará en función de la corriente que circula por cada elemento. Se utiliza para obtener las diferentes corrientes de malla.
Suscribirse a:
Comentarios (Atom)